Inverse kinematic solution: θ1: Premultiply by T10

One side of the equation

T16a = T13 . T34 . T45 . T56 ; T16a // d

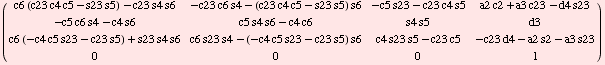
( c6 (c23 c4 c5 - s23 s5) - c23 s4 s6 -c23 c6 s4 - (c23 c4 c5 - s23 s5) s6 -c5 s2 ... 0 0 1

The other side of the equation

T10 = T[dh, 1, 0] ; T10 // d

( c1 s1 0 0 ) -s1 c1 0 0 0 0 1 0 0 0 0 1

T16b = T10 . Trp // FullSimplify ; T16b // d

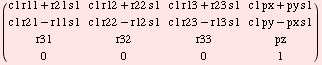
( c1 r11 + r21 s1 c1 r12 + r22 s1 c1 r13 + r23 s1 c1 px + py s1 ) ... r33 pz 0 0 0 1

Both sides of the equation

T16a // d

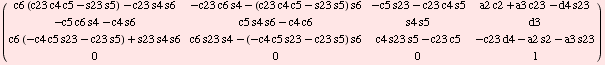
( c6 (c23 c4 c5 - s23 s5) - c23 s4 s6 -c23 c6 s4 - (c23 c4 c5 - s23 s5) s6 -c5 s2 ... 0 0 1

T16b // d

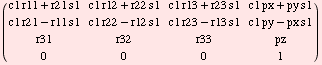
( c1 r11 + r21 s1 c1 r12 + r22 s1 c1 r13 + r23 s1 c1 px + py s1 ) ... r33 pz 0 0 0 1

Note element (2, 4) is just in terms of θ1

eq1 = T16a[[2, 4]] == T16b[[2, 4]] ; eq1 // TF

d3py cos(θ1) - px sin(θ1)

Mathematica solution...

sol1 = Solve[eq1, θ1] ; (θ1 /. sol1)   // TraditionalForm

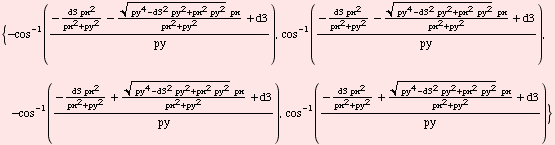
{-cos^(-1)((-(d3 px^2)/(px^2 + py^2) - ((py^4 - d3^2 py^2 + px^2 py^2)^(1/2) px)/(px^2 + py^2) ... -1)((-(d3 px^2)/(px^2 + py^2) + ((py^4 - d3^2 py^2 + px^2 py^2)^(1/2) px)/(px^2 + py^2) + d3)/py)}

How can we solve this by hand?

Make the following substitutions

subs = {px->ρ Cos[ϕ], py->ρ Sin[ϕ]} ; ({#} & /@ subs) //MatrixForm // TF

( pxρ cos(ϕ) ) pyρ sin(ϕ)

eq1a = eq1 /. subs ; eq1a // TF

d3ρ cos(θ1) sin(ϕ) - ρ cos(ϕ) sin(θ1)

Can solve for θ1

eq1b = eq1a[[1]]/ρ == eq1a[[2]]/ρ ; eq1b  //TF

d3/ρ (ρ cos(θ1) sin(ϕ) - ρ cos(ϕ) sin(θ1))/ρ

eq1c = eq1b // Simplify ; eq1c // TraditionalForm

d3/ρ + sin(θ1 - ϕ) 0

Interim solution for θ1

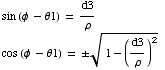
sin (ϕ - θ1) = d3/ρ<br />cos (ϕ - θ1) = ± (1 - (d3/ρ)^2)^(1/2)

    ϕ - θ1 = atan2 (d3/ρ, ± (1 - (d3/ρ)^2)^(1/2))

What is ρ and φ in terms of px and py (by hand)

subs = {px->ρ Cos[ϕ], py->ρ Sin[ϕ]} ; ({#} & /@ subs) //MatrixForm // TF

( pxρ cos(ϕ) ) pyρ sin(ϕ)

sols = {ρ -> (px^2 + py^2)^(1/2), ϕ->ArcTan[px, py]} ; ({#} & /@ sols) //MatrixForm // TF

( 2 2 ) ρ Sqrt[px + py ] -1 ϕ tan (px, py)

Complete solution for θ1

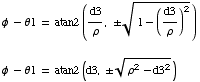
ϕ - θ1 = atan2 (d3/ρ, ± (1 - (d3/ρ)^2)^(1/2)) <br /> ϕ - θ1 = atan2 (d3, ± (ρ^2 - d3^2)^(1/2))

θ1 = atan2 (px, py) -    atan2 (d3, ± ( px^2 +   py^2 - d3^2)^(1/2))

Created by Mathematica  (September 29, 2003)