Inverse kinematic solution: θ3: Some more trickery

The following matrix is now known completely (why?)

T16b // d

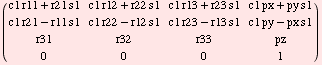
( c1 r11 + r21 s1 c1 r12 + r22 s1 c1 r13 + r23 s1 c1 px + py s1 ) ... r33 pz 0 0 0 1

What can we do next?

Here's what we got on the other side of the equation

T16a// d

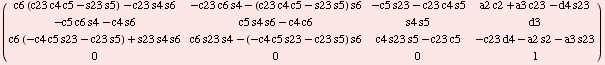
( c6 (c23 c4 c5 - s23 s5) - c23 s4 s6 -c23 c6 s4 - (c23 c4 c5 - s23 s5) s6 -c5 s2 ... 0 0 1

Equate elements (1, 4), (2, 4) and (3, 4):

T16a[[1, 4]] == T16b[[1, 4]] // TF<br />T16a[[2, 4]] == T16b[[2, 4]] // TF <br />T16a[[3, 4]] == T16b[[3, 4]] // TF

a2 cos(θ2) + a3 cos(θ2 + θ3) - d4 sin(θ2 + θ3) px cos(θ1) + py sin(θ1)

d3py cos(θ1) - px sin(θ1)

-d4 cos(θ2 + θ3) - a2 sin(θ2) - a3 sin(θ2 + θ3) pz

Solve for θ2 and θ3. Square and add above equations:

Square elements (1, 4) eqs:

eq1b = (T16a[[1, 4]])^2 == (T16b[[1, 4]])^2 ; eq1b // TF

(a2 cos(θ2) + a3 cos(θ2 + θ3) - d4 sin(θ2 + θ3))^2 (px cos(θ1) + py sin(θ1))^2

Square elements (2, 4) eqs:

eq1a = (T16a[[2, 4]])^2 == (T16b[[2, 4]])^2 ; eq1a // TF

d3^2 (py cos(θ1) - px sin(θ1))^2

Square elements (3, 4) eqs:

eq1c = (T16a[[3, 4]])^2 == (T16b[[3, 4]])^2 ; eq1c // TF

(-d4 cos(θ2 + θ3) - a2 sin(θ2) - a3 sin(θ2 + θ3))^2pz^2

Add them all up:

eq2 = eq1a[[1]] + eq1b[[1]] + eq1c[[1]] == eq1a[[2]] + eq1b[[2]] + eq1c[[2]] ; eq2 // TF

d3^2 + (-d4 cos(θ2 + θ3) - a2 sin(θ2) - a3 sin(θ2 + θ3))^2 + (a2 cos( ... ;3))^2pz^2 + (py cos(θ1) - px sin(θ1))^2 + (px cos(θ1) + py sin(θ1))^2

Simplify:

eq3 = FullSimplify [eq2] ; eq3 // TF

a2^2 + 2 a3 cos(θ3) a2 + a3^2 + d3^2 + d4^2px^2 + py^2 + pz^2 + 2 a2 d4 sin(θ3)

No longer dependent on θ2! Lump all constants together, and we have simple eq. in terms of θ3:

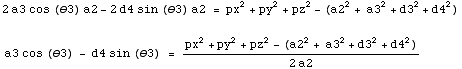
2 a3 cos (θ3) a2 - 2 d4 sin (θ3) a2 = px^2 + py^2 + pz^2 - (a2^2 + a3^2 + d3^2 + d4^ ... > a3 cos (θ3) - d4 sin (θ3) = (px^2 + py^2 + pz^2 - (a2^2 + a3^2 + d3^2 + d4^2))/(2a2)

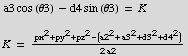
a3 cos (θ3) - d4 sin (θ3) = K <br /> K =    (px^2 + py^2 + pz^2 - (a2^2 + a3^2 + d3^2 + d4^2))/(2a2)

Very similar to equation for θ1:

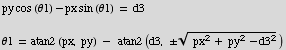
py cos (θ1) - px sin (θ1) = d3<br /> θ1 = atan2 (px, py) -    atan2 (d3, ± ( px^2 +   py^2 - d3^2)^(1/2))

So, the solution for θ3 is:

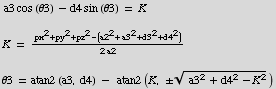
a3 cos (θ3) - d4 sin (θ3) = K<br /><br />K =    (px^2 + py^2 + pz^2 - (a2 ... ) <br /><br />θ3 = atan2 (a3, d4) -    atan2 (K, ± ( a3^2 + d4^2 - K^2)^(1/2))

Created by Mathematica  (September 29, 2003)