Section 1: Two-link planar manipulator

DH parameters

DH = {{0, 0, 0, θ1, 0}, {0, L1, 0, θ2, 0}, {0, L2, 0, 0, 0}} ; DH //TraditionalForm

( 0 0 0 θ1 0 ) 0 L1 0 θ2 0 0 L2 0 0 0

Numeric values for simulation

nDH = DH /. {L1 -> 1, L2 -> 1/2} // N ; nDH // TraditionalForm

( 0.` 0.` 0.` θ1 0.` ) 0.` 1.` 0.` θ2 0.` 0.` 0.5` 0.` 0.` 0.`

Nonsingular inverse Jacobian trajectory

This section simulates the relationship Overscript[θ, .] = J^(-1) Overscript[X, .]for a non-singular, circular, end-effector trajectory.

RowBox[{RowBox[{pick = {1, 1} ;, , (* select first two rows of Jacobian *), <br />, RowBox[{R ... } // N ;, , (* initial joint angles *), <br />, maxTime = 2Pi // N ;}], (* simulation length *)}]

traj = SIJVT[ nDH, pick, path1, init1, maxTime] ;

Square Jacobian: Using Inverse[ ]

AnimateTrajectory[nDH, traj, 2] ;

[Graphics:../anim1.gif]

Singular inverse Jacobian trajectory

This section simulates the relationship Overscript[θ, .] = J^(-1) Overscript[X, .]for a straight-line end-effector trajectory that results in a singularity.

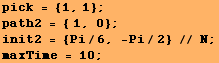
pick = {1, 1} ; path2 = { 1, 0} ; init2 = {Pi/6, -Pi/2} // N ; maxTime = 10 ;

traj = SIJVT[ nDH, pick, path2, init2, maxTime] ;

Square Jacobian: Using Inverse[ ]

NDSolve :: ndsz : At t == 0.38247792793252683`, step size is effectively zero; singularity or stiff system suspected. More…

AnimateTrajectory[nDH, traj, 2] ;

[Graphics:../anim2.gif]

Joint velocities Overscript[θ, .] _1 andOverscript[θ, .] _2

endTime = traj[[1, 1, 1, 2]] ;

{vθ1, vθ2} = {D[traj[[1]][t], t], D[traj[[2]][t], t]} ;

Plot[{vθ1, vθ2}, {t, 0, endTime}, FrameTrue, PlotStyle {RGBColor[1, 0, 0], RGBColor[0, 0, 1]}] ;

[Graphics:../HTMLFiles/index_73.gif]

Created by Mathematica  (October 1, 2003)